Skyboxes have limitations. They have a finite number of pixels. The further you zoom in, the bigger those pixels get. So what do you do if you're making a space game and want a telescope? Stars should be small both when zoomed in and when zoomed out.
First, a quick lesson: how big is a star? Well, Proxima Centauri is 107,280 km radius. It is also 40,174,990,000,000 km away from earth. This means it has an angular size of 0.00055 arc-seconds (2.67e-09 radians). This is tiny. Like so tiny that even the james web space telescope's impressive 0.07 arcseconds of angular resolution is a couple orders of magnitude short. Ie: a star (ignoring lens artifacts, ccd bloom etc. etc.) should still be a single pixel.
So if a star should always be exactly one pixel in size, how do we render them? Clearly a skybox won't work at narrow zoom angles, so what can we do? One option is to use geometry, and to use a vertex shader to adjust the scale of the star t always be small. However, if we want millions of stars (and remember, there are 100 billion in our galaxy alone), then that is a lot of GPU time. So can we do it in a single shader? Yep, turns out you can.
The naive way of rendering lots of dots in a shader is to calculate the distance to all of them. This has the limitation that again you are iterating, and a billion of anything is a lot (a Ghz is a billionth of a second, so if you can render one star per cycle, a billion stars takes one second). But there is another solution: if we can divide up the sky into small chunks and have each chunk render exactly one star, then... we only have to render one star per pixel.
Dividing up the Sky
So how do you divide up the sky into equal area chunks. This is something of an open mathematical problem to solve it perfectly, but we don't have to be perfect, we just have to be good enough.
My first pass was to use a 3D grid, and intersect that with a sphere.
This looks like:
(Look at the random colors, not the lat/long lines. That's just to show
you it's a sphere).
We can move the grid points and do a voroni on them and it gets, uh, different.
Still some very unequal areas here. I tried a spiral as well as parabaloid mapping,
but it's hard to get coordinates inside those cells, so I settled on a cube map:
This is pretty good, but you can see that towards the corners the perspective makes
the cells smaller.
After some fiddling, I discovered this very simple distortion:
float d_edge = 2.0 - max(abs(uv.x), abs(uv.y));
uv *= sqrt(d_edge);
This "pulls in" the corners:
The cells get a bit distorted, but a lot less than before.
Oh yeah, and we need the coordinates within each cell as well:
Drawing the stars
If we have coordintes for each cell we can put a star in each cell
by computing the distance to the cell center and applying some color:
And here's the important part:
We can now scale the radius of each dot by the camera's zoom
innerCoords = abs(innerCoords - 0.5) * 2.0;
float dist = length(innerCoords) * iResolution.y;
float radius = max(1.0 - dist / (numCells * lens * STAR_RADIUS), 0.0);
(the lens variable represents the FOV, and iResolution is the screen resolution)
It's also wise to make the stars grid a bit less obvious by turning some
stars off and moving them inside the cells by a small amount to break up
lines:
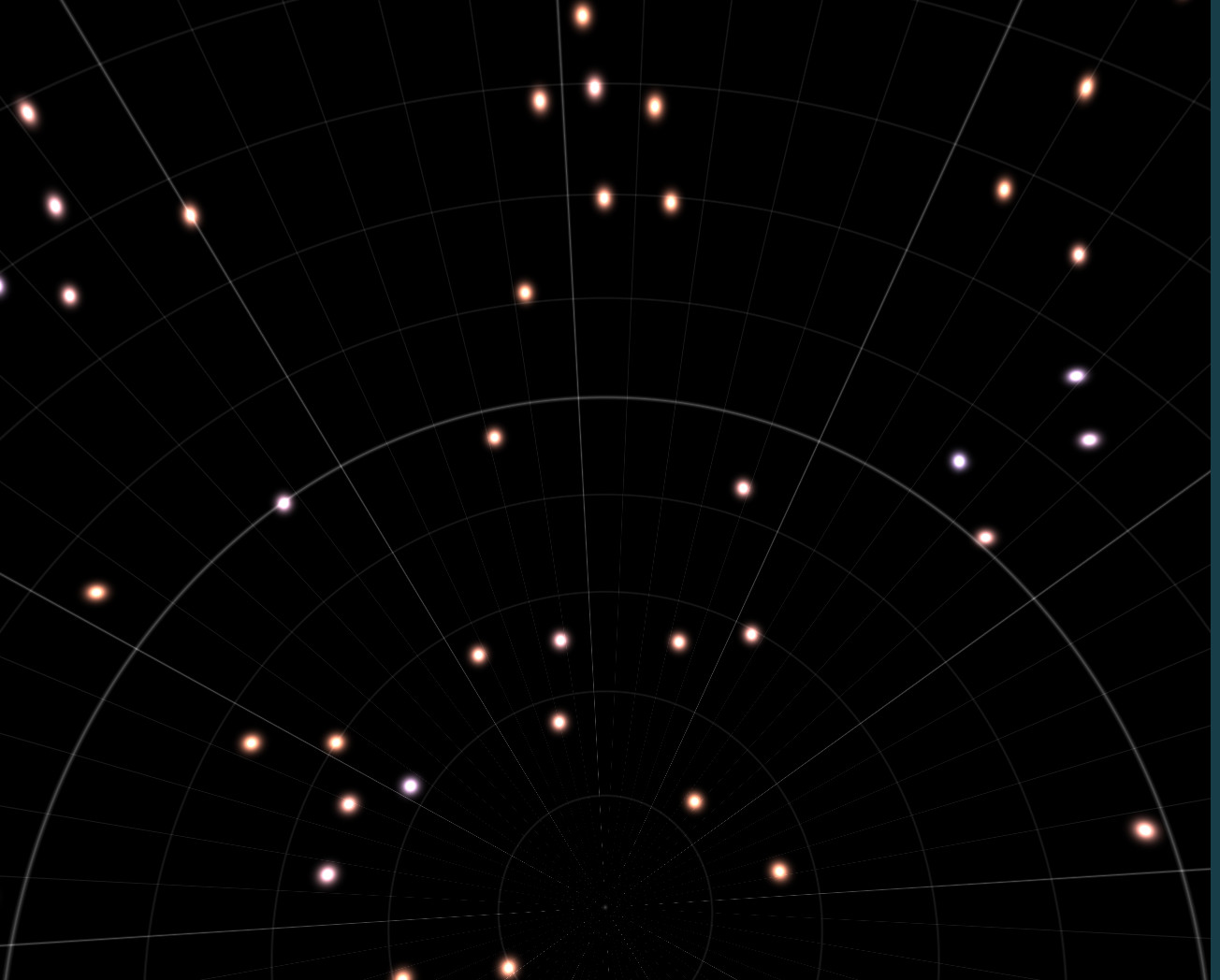
How many stars?
If we want to avoid needing to do subpixel rendering, each cell needs to be a minimum of a couple pixels on the screen. This means that the number of stars depends on the widest angle we need to render and the resolution of the monitor. I found a nice number was 200 cells per face of the cube. This works well even at quite low screen resolutions (600px or so), and is stable (no flickering as you move the camera)
You can then do a couple "layers" of stars with different noise and
cell counts in order to increase the number of stars. I settled
for 9 layers of stars.
If we didn't have the density map controlling where the stars were, this
would be:
num_stars = num_cell_divisions * num_cell_divisions * num_sides_of_cube * num_layers
num_stars = 200 * 200 * 6 * 9
num_stars = 2,160,000
That is 2 million stars.
So how to get to a billion?
One way would be to increase the number of cells to ~6000 per edge. This would work fine on an 8k monitor with no other changes required ;). 6000 per edge would work fine when more zoomed in even on more normal screens, so one option would be to fade in a high density star map as you zoom. You may have to twiddle with brightnesses so you don't go "huh, I should have seen that star" - probably few bright stars always visible and then layers of increasing density but decreasing brightness that fade in as you zoom.
Anyway, that's all for now. Here's the whole shadertoy shader:
/*
CLICK AND DRAG TO LOOK AT ANOTHER PART OF THE SKY
I'm building a semi-realistic space game and discovered that a skybox looks terrible
when you are using a telescope with a lens angle of 1 degree. Why? Well, stars are
really really far away and the light is parallel. This means that (almost) no matter
how far you zoom in on them ... they stay the same angular size.
This means that any sort of normal skybox falls apart when you zoom because ... the
stars will get bigger (or when you zoom out the stars will alias).
My aims are:
- Render a sky full of stars
- Handle dynamic zooming - stars should stay small as you zoom
- Have enough stars that at high zoom levels (ie a telescope) it is still
interesting enough.
- Flicker free when moving the viewport (ie no obvious aliasing)
- Artistic control ("paint stars here")
There are two interesting effects I noticed:
- As you zoom out you see more stars at the same brightness, so the scene
gets visually lighter. This is the opposite to "normal" where a bright object
occupies more of the scene as you zoom in. I correct for this by tweaking
the camera's exposure which has the nice property of seeing
more stars as you zoom in.
The same applies to higher resolution screens. A higher resolution screen
has more pixels with fewer lit.
- Mostly you don't have to worry about the stars aliasing as they stay the same size
on screen.
Placing stars randomly on a sphere is somewhat hard. This is my second attempt, and I divide
up the world into a using a cubmap (distorting it to keep more equal areas).
This is then divided into cells and a star placed in each cell. Rather than voroni the
cells I went for multiple layers - It doesn't require that many more calculations to do a full
star render vs sampling a bunch of cells, so why not render 8 times more stars rather
than doing 8 voroni samples?
How many stars are there in this scene? If you disable the density map there are:
200 * 200 * 6 * 9 = 2,160,000
There is definitely still room to improve this:
- if you disable the density map you can see regular lines in certain places in the
skybox. I think this is due to limiting how far each cell can offset the star, and
that all the cells are about the same size.
- MOR STARZ. I want clouds of them. Ther eare 100 billion stars in the milky way.
I'm still an order of magnitude off them in terms of count, and probably even
more so in terms of density in some areas of the sky.
One possible solution here is that zooming in could inveil another layer of stars
with a much higher cell count (this would cause aliasing if visible when zoomed out).
If a layer can be done at 1000 cells, this is the same as a couple billion stars
on a single layer
- It may be worth revising voroni.
- Can the number of density map samples be reduced?
I also tried dual paraboloid maps as a star placement, but when looking at the UV coords,
I think it would have a fairly obvious seam.
- sdfgeoff
*/
const float PI = 3.14159;
const float MAJOR_LINES = 6.0;
const float MAJOR_LINE_WIDTH = MAJOR_LINES * 0.002;
const float MINOR_LINES = MAJOR_LINES * 5.0;
const float MINOR_LINE_WIDTH = MINOR_LINES * 0.001;
const float MAJOR_LINE_INTENSITY = 0.2;
const float MINOR_LINE_INTENSITY = 0.1;
// How large should a star be?
const float STAR_RADIUS = 10.0;
// Higher = fewer bright stars
const float STAR_GAMMA = 20.0;
float hash12(vec2 p)
{
vec3 p3 = fract(vec3(p.xyx) * .1031);
p3 += dot(p3, p3.yzx + 33.33);
return fract((p3.x + p3.y) * p3.z);
}
vec3 hash33(vec3 p3)
{
p3 = fract(p3 * vec3(.1031, .1030, .0973));
p3 += dot(p3, p3.yxz+33.33);
return fract((p3.xxy + p3.yxx)*p3.zyx);
}
float sphere_lines(float angle, float elevation) {
float lines = 0.0;
lines += clamp((abs(fract(elevation / PI * MAJOR_LINES) - 0.5) * 2.0 - 1.0 + MAJOR_LINE_WIDTH) / MAJOR_LINE_WIDTH, 0.0, 1.0) * MAJOR_LINE_INTENSITY;
lines += clamp((abs(fract(angle / PI * MAJOR_LINES) - 0.5) * 2.0 - 1.0 + MAJOR_LINE_WIDTH) / MAJOR_LINE_WIDTH, 0.0, 1.0) * MAJOR_LINE_INTENSITY;
lines += clamp((abs(fract(elevation / PI * MINOR_LINES) - 0.5) * 2.0 - 1.0 + MINOR_LINE_WIDTH) / MINOR_LINE_WIDTH, 0.0, 1.0) * MINOR_LINE_INTENSITY;
lines += clamp((abs(fract(angle / PI * MINOR_LINES) - 0.5) * 2.0 - 1.0 + MINOR_LINE_WIDTH) / MINOR_LINE_WIDTH, 0.0, 1.0) * MINOR_LINE_INTENSITY;
return lines;
}
// Converts from a 3D direction vector into a 2D UV map with equal(ish) area
// The UV is not constrained to the 0-1 range
vec2 to_cells(vec3 rayDirection) {
// Cubemap
vec3 norm = normalize(rayDirection);
vec3 absnorm = abs(norm);
vec2 uv = vec2(0,0);
float face = 0.0;
if (absnorm.x / absnorm.z < 1.0 && absnorm.y / absnorm.z < 1.0) {
uv = norm.xy / absnorm.z;
face = step(0.0, norm.z);
}
if (absnorm.x / absnorm.y < 1.0 && absnorm.z / absnorm.y < 1.0) {
uv = norm.xz / absnorm.y;
face = step(0.0, norm.y) + 2.0;
}
if (absnorm.y / absnorm.x < 1.0 && absnorm.z / absnorm.x < 1.0) {
uv = norm.yz / absnorm.x;
face = step(0.0, norm.x) + 4.0;
}
// Inflate the cube to reduce distortion due to corners.
// I kinda stubled over this one experimentally, no idea if it has a name, but
// it works quite well at making the cells closer to equal area.
// It's probably got a name.
float d_edge = 2.0 - max(abs(uv.x), abs(uv.y));
uv *= sqrt(d_edge);
return uv * 0.5 + 0.5 + vec2(face, 0.0);
}
vec3 stars(vec2 uv, float lens, float seed, float numCells) {
vec2 rawCells = uv * numCells;
vec2 cellId = floor(rawCells);
float starDensity = pow(textureLod(iChannel0, cellId / numCells, 0.0).r + 0.2, 4.0);
vec2 innerCoords = fract(rawCells);
vec3 offsets = hash33(vec3(cellId, seed));
innerCoords += (offsets.xy - 0.5) * 0.5;
innerCoords = abs(innerCoords - 0.5) * 2.0;
vec4 data = vec4(
length(innerCoords),
offsets
);
float dist = data.x * iResolution.y;
float radius = max(1.0 - dist / (numCells * lens * STAR_RADIUS), 0.0);
float intensity = pow(radius, 4.0); // Falloff - bright in center
intensity *= pow(data.y, STAR_GAMMA); // more dim stars than bright ones
intensity *= step(data.w, starDensity);
return intensity * mix(
vec3(0.8, 0.5, 0.4),
vec3(0.7, 0.6, 0.8),
pow(data.z, 2.0) // more red stars than blue ones
) * 4.0;
}
vec3 world_background(vec3 rayDirection, float lens) {
vec3 col = vec3(0.0);
vec2 cells = to_cells(rayDirection);
col += stars(cells, lens, 1.0, 200.0) * 4.0;
col += stars(cells, lens, 2.0, 199.0) * 0.8;
col += stars(cells, lens, 3.0, 198.0) * 0.7;
col += stars(cells, lens, 4.0, 197.0) * 0.6;
col += stars(cells, lens, 5.0, 196.0) * 0.5;
col += stars(cells, lens, 6.0, 201.0) * 0.4;
col += stars(cells, lens, 7.0, 202.0) * 0.3;
col += stars(cells, lens, 8.0, 203.0) * 0.2;
col += stars(cells, lens, 9.0, 190.0);
// Increase Exposure as zoom in
col *= (0.3 / lens);
float r2 = dot(rayDirection.xy, rayDirection.xy);
float elevation = acos(rayDirection.z / sqrt(r2 + rayDirection.z * rayDirection.z));
float angle = atan(rayDirection.y, rayDirection.x);
float lines = sphere_lines(angle, elevation);
return col + lines;
}
vec4 QuatFromAxisAngle(vec3 axis, float angle)
{
float hA = angle * 0.5;
float s = sin(hA);
float c = cos(hA);
return vec4(axis*s, c);
}
vec4 QuatMul(vec4 q, vec4 r)
{
vec4 nq;
nq.x = q.w * r.x + q.x * r.w + q.y * r.z - q.z * r.y;
nq.y = q.w * r.y - q.x * r.z + q.y * r.w + q.z * r.x;
nq.z = q.w * r.z + q.z * r.w - q.y * r.x + q.x * r.y;
nq.w = q.w * r.w - q.x * r.x - q.y * r.y - q.z * r.z;
return nq;
}
mat4 QuatToMat(vec4 q)
{
float xx = q.x * q.x, yy = q.y * q.y, zz = q.z * q.z;
float xy = q.x * q.y, yz = q.y * q.z, xz = q.x * q.z;
float xw = q.x * q.w, yw = q.y * q.w, zw = q.z * q.w;
return mat4(1.-2.*(yy+zz),2.*(xy-zw),2.*(xz+yw),0.,2.*(xy+zw),1.-2.*(xx+zz),2.*(yz-xw),0.,2.*(xz-yw),2.*(yz+xw),1.-2.*(xx+yy),0.,0.,0.,0.,1.);
}
mat3 QuatToMat3(vec4 q)
{
float xx = q.x * q.x, yy = q.y * q.y, zz = q.z * q.z;
float xy = q.x * q.y, yz = q.y * q.z, xz = q.x * q.z;
float xw = q.x * q.w, yw = q.y * q.w, zw = q.z * q.w;
return mat3(1.-2.*(yy+zz),2.*(xy-zw),2.*(xz+yw),2.*(xy+zw),1.-2.*(xx+zz),2.*(yz-xw),2.*(xz-yw),2.*(yz+xw),1.-2.*(xx+yy));
}
mat4 createCameraRotationMatrix(vec2 vSUV)
{
vec4 u = QuatFromAxisAngle(vec3(0., 0., 1.), vSUV.x);
vec4 v = QuatFromAxisAngle(QuatToMat3(u) * vec3(1., 0., 0.), vSUV.y);
return QuatToMat(QuatMul(u,v));
}
void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
// Normalized pixel coordinates (from 0 to 1)
vec2 raw_uv = fragCoord/iResolution.xy;
vec2 uv = raw_uv;
uv = (uv - 0.5) * 2.0;
uv.x *= iResolution.x / iResolution.y;
// Render our geometry
vec2 vSphericalUV = (iMouse.xy / iResolution.xy) * 4.0;
vSphericalUV.y = clamp(vSphericalUV.y,0.,PI); //Clamp to avoid upside down camera.
mat4 camera_transform = createCameraRotationMatrix(vSphericalUV);
vec3 start_point = camera_transform[3].xyz;
float LENS = sin(iTime) * 0.3 + 0.305;
vec3 direction = normalize(vec3(uv * LENS, 1.0));
direction = (camera_transform * vec4(direction, 0.0)).xyz;
// Output to screen
fragColor = vec4(world_background(direction, LENS),1.0);
}